Littlewood’s Three Principles (3/3)

So far we’ve proven Littlewood’s first and third principles. In this last installment, we’ll prove his second principle, that “every function is nearly continuous.” This result is better known as Lusin’s Theorem.

From now on, we will let $\mu^d$ denote Lebesgue measure on $\mathbb{R}^d$ . We’ll state two basic theorems, whose proofs make great exercises:

Theorem If $\{f_n\}_{n=1}^{\infty}:\mathbb{R}^d\to \mathbb{R}$ are continuous and converge uniformly to $f$ , then $f$ is continuous.

Theorem If $f$ is measurable on $\mathbb{R}^d$ , then there exists a sequence of step functions $\{\psi_n\}_{n=1}^{\infty}$ that converges pointwise to $f(x)$ for almost every $x$ .

These theorems are true in much more generality. But these watered-down statements are all that we need.

Theorem (Luzin’s Theorem) Suppose $f$ is measurable and finite valued on a finitely-measured subset $A$ of $\mathbb{R}^d$ . Then for every $\epsilon>;0$ there exists a closed set $B$ with

$B\subset A$ and $\mu^d(A\setminus B)<;\epsilon$

such that $f\mid_{B}$ is continuous.

Proof. The idea is to approximate $f$ pointwise almost everywhere with a sequence of step functions. Outside a set of small measure, the set functions are continuous. So then by Egorov’s Theorem, outside a set of small measure, $f$ is the uniform limit of continuous functions, and so $f$ is continuous.

To this end, let $\{\psi_n\}_{n=1}^{\infty}$ be a sequence of step functions so that $\psi_n\to f$ almost everywhere. Let $\epsilon>;0$ . Now for each $n\in \mathbb{N}$ , find some measurable $E_n$ for which $\mu^d(E_n)<;\frac{\epsilon}{2^{n+1}}$ and $\psi_n$ is continuous outside of $E_n$ (Why can we do this?). Then each $\psi_n$ is continuous outside of $E=\cup_{n=1}^{\infty}E_n$ , whose measure is at most $\sum_{n=1}^{\infty}\frac{\epsilon}{2^{n+1}}=\frac \epsilon 2$ . Hence each $\psi_n$ is continuous on $A\setminus E$ .

Since $A\setminus E$ is finitely measured, and $\{\psi_n\}_{n=1}^{\infty}$ converges to $f$ pointwise on $A\setminus E$ , by Egorov’s theorem there exists a subset $B\subseteq A\setminus E$ with

$\mu^d((A\setminus E)\setminus B)<; \frac \epsilon 2$

for which $f$ is the uniform limit of $\{\psi_n\}_{n=1}^{\infty}$ on $B$ . But each $\psi_n$ is continuous on $B$ and so $f\mid_B$ is continuous, being the uniform limit of continuous functions. Since $B\subseteq A\setminus E$ , we have

$\mu^d(A\setminus B)= \mu^d((A\setminus E)\setminus B)+\mu^d(E) <;\frac \epsilon 2 + \frac \epsilon 2=\epsilon$

as claimed. Lastly, we may assume without loss of generality that $B$ is closed, for otherwise we could, by Littlewood’s First Principle, approximate it’s complement with a finite union of open sets and take $B$ to be the closed complement of that union.

This completes this series on Littlewood’s three principles. Thanks for reading.

2 Responses to Littlewood’s Three Principles (3/3)

Ryan says:

05/26/2012 at 23:59

I think that in the first theorem you mean to say if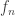 $f_n$ converge to $f$ uniformly then $f$ is continuous.

- Adam Azzam says:
  
  05/27/2012 at 00:05
  
  Ha! If only what I wrote was true. Good catch Hotovy. I updated it.