Wow, it’s been a long time since my last post. Sorry about that. I intend (though I’ll make no promises) to post a bit more regularly now.
This final post in my ac series was advertised to be a post about surprising uses of choice, but it’s grown to be a general discussion of ac.
— 1. Important principles weaker than full ac —
To start developing a picture of how ac relates to other mathematical assertions, we need to describe some so-called choice principles that are not provable in zf but are weaker than ac. (See the previous two posts in this series (I and II) for some assertions equivalent to ac.)
One of the most natural ways to weaken ac is to limit the number of choices you’re making or the size of the bins you’re choosing from. By this sort of weakening we come to one of the mildest choice principles, the Axiom of Countable Choice:
Definition 1. The Axiom of Countable Choice (acω) asserts that every countable family of nonempty sets has a choice function. (That is, if  and
and  is countable, then there is a function that assigns each member
is countable, then there is a function that assigns each member  of
of  a member of
a member of  .)
.)
acω is substantially weaker than ac, but it’s sufficient to forbid many types of unpleasant sets. For example, it is a theorem of zf+acω that every infinite set has a countable subset, though this isn’t provable in zf alone (that is, there is a model of zf in which there is an infinite set with no countable subset). Many elementary facts about the real numbers can be established in zf+acω; for example, only zf+acω is necessary to prove that a countable union of countable sets is countable (though, again, some form of choice is necessary to prove this). In particular, in the presence of acω, 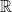 is not a countable union of countable sets. (Apparently the assertion the countable union of countable sets is countable is actually strictly weaker than acω. I think I once found a reference for this.)
is not a countable union of countable sets. (Apparently the assertion the countable union of countable sets is countable is actually strictly weaker than acω. I think I once found a reference for this.)
We need slightly more firepower to do real analysis properly, though. Proofs in (baby) real analysis often require the construction of a sequence, which is typically built inductively by choosing the  th term from, e.g., a ball of radius
th term from, e.g., a ball of radius  . The proof of the Baire Category Theorem is a good example of this style of argument, which uses the Axiom of Dependent Choice:
. The proof of the Baire Category Theorem is a good example of this style of argument, which uses the Axiom of Dependent Choice:
Definition 2. The Axiom of Dependent Choice (dc) is the following assertion: If 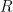 is a relation on a nonempty set
is a relation on a nonempty set  such that for every
such that for every  there is a
there is a 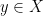 such that
such that  , then there is a sequence
, then there is a sequence  , of members of
, of members of  such that
such that  for every
for every 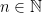 .
.
Apparently this paper gives a proof that the Baire Category Theorem is equivalent (in zf, of course) to dc.
It is straightforward to show that dc implies acω (exercise!). There are many choice principles (like dc and acω) that guarantee only the existence of choice functions for sets satisfying certain size restrictions. (acω restricts the size of the family; other useful choice principles restrict the size of each member of the family.) dc is sufficient to prove the results of basic analysis and is particularly appealing because it is too weak to prove that nasty things like nonmeasurable sets and Banach–Tarski decompositions of the sphere exist. (See section 2 below.)
Notice that acω and dc are local principles, in the sense that they are chiefly concerned with sets of cardinality near 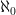 (this is less true of dc). For this reason, it shouldn’t be surprising that each of them is strictly weaker than full ac. Applications outside analysis often require global principles (for sets or spaces of arbitrary cardinality, e.g.), and a popular global choice principle weaker than full ac is the Ultrafilter Lemma.
(this is less true of dc). For this reason, it shouldn’t be surprising that each of them is strictly weaker than full ac. Applications outside analysis often require global principles (for sets or spaces of arbitrary cardinality, e.g.), and a popular global choice principle weaker than full ac is the Ultrafilter Lemma.
Definition 3. The Ultrafilter Lemma (ul) asserts that every filter on a set can be extended to an ultrafilter.
The Prime Ideal Theorem (pit) asserts that every boolean algebra has a prime ideal, an ideal 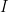 such that
such that  or
or 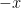 is a member of
is a member of 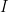 for every
for every  .
.
Conveniently, the ul is equivalent to other interesting choice principles.
Theorem 4. In zf, the following are equivalent:
- The Ultrafilter Lemma;
- The Prime Ideal Theorem;
- The Compactness Theorem for first-order logic.
The proof of this theorem isn’t too difficult, so I won’t provide it here. We are taking on faith that the ul is strictly weaker than ac, but it would be nice to have a sense of just how much weaker it is. We have several different equivalent formulations of ac, each about a different sort of mathematical object:
Theorem 5. In zf, the following are equivalent:
- ac;
- Every set can be wellordered;
- Tychonoff’s Theorem: a product of compact spaces is compact;
- Every vector space has a basis.
(By the way, Exercise: prove that Tychonoff’s theorem implies ac. The proof I know of is short but requires a trick.)
By transferring choice principles over to new contexts (like topology) using the ideas from the proof that the assertions above are equivalent, we can provide a satisfying picture of how much weaker the ul is than ac.
Theorem 6. In zf, the following are equivalent:
- the ul;
- Every product of compact Hausdorff spaces is compact;
- Every product of 2 is compact.
[Edit (Nov 10 2012): the ul is not equivalent to the assertion that every set can be linearly ordered or ac with finite `bins’; in fact,
ul 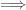 every set can be linearly ordered
every set can be linearly ordered 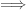 ac with finite bins,
ac with finite bins,
but none of those implications is reversible. It has recently come to my attention (I believe it’s proved in this paper) that the ul is equivalent to Tychonoff’s Theorem for sober spaces.]
Exercise: (Since so many of our authors and readers are analysts) The pit implies Hahn–Banach. (This is apparently difficult, so comment if you think you have a solution. But don’t give it away; I haven’t thought about it much yet.)
— 2. Math(s) without choice —
I’ll say a few words about two results whose proofs don’t require choice, the Cantor–Schroeder–Bernstein Theorem and Ramsey’s Theorem.
That the csb doesn’t require choice is surprising; its conclusion asserts the existence of a function constructed rather mysteriously from the functions in its hypothesis. Of course, it’s easy to say ‘Obviously it doesn’t require choice: here’s a proof that doesn’t use it!’, but when you suppress the intuition you gain by understanding the proof of the csb, the surprise returns. One reason to expect this surprise is that the easiest proof of the csb in zfc (namely, reduce to the case when your sets are wellordered by appealing to ac) makes unavoidable use of choice. And csb provides a mysterious function, which is what ac usually does.
The dual csb theorem, which asserts that if there are surjections 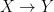 and
and 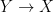 then there is a bijection
then there is a bijection 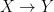 (and is a theorem of zfc), is not provable in zf. Apparently it is an open question whether the dual csb implies ac.
(and is a theorem of zfc), is not provable in zf. Apparently it is an open question whether the dual csb implies ac.
Maybe it’s not so surprising that Ramsey’s Theorem doesn’t require ac, but it can be made into a nontrivial choice principle by recasting it as ‘For every  -coloring of the
-coloring of the  -subsets of an infinite set
-subsets of an infinite set  , there is an infinite monochromatic subset
, there is an infinite monochromatic subset  of
of  .’ (‘But can’t you just prove this from the normal statement of Ramsey’s Theorem by restricting to a countable subset of
.’ (‘But can’t you just prove this from the normal statement of Ramsey’s Theorem by restricting to a countable subset of  ?’, you ask? Remember that it is not provable in zf that every infinite set has a countable subset!)
?’, you ask? Remember that it is not provable in zf that every infinite set has a countable subset!)
One final note: Solovay proved that it is consistent with zf+dc that every subset of 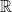 is (Lebesgue-)measurable. So we can do analysis somewhat familiarly in a setting where all of the standard theorems (Heine–Borel, etc.) are true, but pathological nasties like nonmeasurable sets don’t exist. What does such analysis look like? I don’t know, but I’d like to.
is (Lebesgue-)measurable. So we can do analysis somewhat familiarly in a setting where all of the standard theorems (Heine–Borel, etc.) are true, but pathological nasties like nonmeasurable sets don’t exist. What does such analysis look like? I don’t know, but I’d like to.
— 3. Obviously true? —
The temptation at this point, I think, is to point out theorems we are unable to prove without full ac, and then argue that any theory strictly weaker than zfc provides a somehow deficient concept of set, since it is unable to prove those theorems. My objection to this attitude is that there is a lot of choiceless mathematics to be understood (and alternative extensions of zf (e.g., by the Axiom of Determinacy) that are capable of proving quite powerful, interesting theorems) and we simply gain nothing by asserting (or believing or whatever) that some set of axioms is the gods-given ‘correct’ one and that we should blindly stick to it (in the same way, more absurdly, that a commutative algebraist gains nothing by asserting with religious fervor that noncommutative rings simply don’t exist, in whatever metaphysical sense). Anyway, this is a standard platonism-versus-pluralism issue, and philosophers of mathematics spend a lot of time thinking about it.
— 4. The ‘magic wand’ factor —
Another reason to be careful about (though not necessarily avoid altogether) use of ac is that it is notorious for clouding the ideas in proofs. For example, consider the standard proof in zfc that every countable union of countable sets is countable: Take a countable set of sets 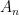 , choose (by acω) an enumeration of each one, and zigzag through the enumerations just as in the proof that
, choose (by acω) an enumeration of each one, and zigzag through the enumerations just as in the proof that  is countable. Contrast that statement and proof to the following:
is countable. Contrast that statement and proof to the following:
Theorem 7. The counted union of counted sets is counted. That is, if 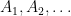 are countably many sets, and for each
are countably many sets, and for each  the function
the function 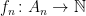 is a bijection, then there is a bijection
is a bijection, then there is a bijection  (and we can write down a formula for it in terms of the
(and we can write down a formula for it in terms of the  ).
).
And, of course, the proof is the same as above, except that the enumerations are already chosen for us. My point is that the standard statement and proof hide the real idea, which is the construction of 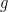 from the
from the  . If you want the stronger result, just take this theorem and snort the necessary amount of choice. Separating the choice-snorting from the real work gives us a deeper understanding of the result and its proof. Assuming ac carelessly is in the same spirit—though hardly as ridiculous—as assuming
. If you want the stronger result, just take this theorem and snort the necessary amount of choice. Separating the choice-snorting from the real work gives us a deeper understanding of the result and its proof. Assuming ac carelessly is in the same spirit—though hardly as ridiculous—as assuming 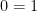 would be: you can prove many things, but without understanding your subject as deeply as you would otherwise. (I should mention that I owe this example, related insight, and the expression ‘snorting choice’ to Thomas Forster.)
would be: you can prove many things, but without understanding your subject as deeply as you would otherwise. (I should mention that I owe this example, related insight, and the expression ‘snorting choice’ to Thomas Forster.)
Recently I encountered another similar example, which I’ll quickly share. I mentioned earlier that the Baire Category Theorem is a theorem of zf+dc. The BCT for separable completely metrizable spaces is actually a theorem of zf. (This isn’t hard to prove, so you should do it if you’re interested. The point is that the countable dense set allows you to make your choices canonical, since you can always take from the countable dense set the lowest-indexed point that does what you need it to do. I think this is a standard trick for proving things about topological spaces without ac, but I don’t know of another example.) I don’t know of a way to get to full BCT from BCT for separable spaces by invoking dc, though, so this isn’t as good an example as the previous one.
— 5. Coming attractions —
I’ve recently gotten excited about infinitary combinatorics, so that will probably be the topic of my next major series. Combinatorial set theory should also show up soon, as will some set-theoretic topology.
I’ll almost certainly write about toposes [sic!] someday, too, but not until after I’ve written a post or two about general category theory.
In other news, Jay has promised to write a post in the next ten days, so stay tuned! P.S. This post is the first I’ve written using Luca Trevisan’s fantastic latex2wp. I recommend it to all math WordPress bloggers! (Quick test: Does WordPress render Erdős correctly? Yes.) Blue, no green!
Two standard references, from which most of this material comes:
Jech, Thomas J. The Axiom of Choice. 2008 Dover edition, originally published as: Studies in Logic and the Foundations of Mathematics, Vol. 75. North-Holland Publishing Co., Amsterdam-London; American Elsevier Publishing Co., Inc., New York, 1973. xi+202 pp. (MR0396271)
Howard, Paul; Rubin, Jean E. Consequences of the axiom of choice. Mathematical Surveys and Monographs, 59. American Mathematical Society, Providence, RI, 1998. viii+432 pp. (MR1637107)
-adic representations of integers. If
is any integer (technically we should assume
, it doesn’t really matter), and if
is a prime number, then
can be written (uniquely) as
, where
are integers. This is easy to prove using the fundamental theorem of arithmetic and the division algorithm. Without further adieu I give you the following
be a prime number and
. Then
and
are the
-adic representations of
and
.
, we have the identity
. Working modulo
, we have
in this expansion is
. On the other hand, if we expand the product on the right, it’s easy to see that no two terms in the product will have the same power of
. Thus, to compute the coefficient of
in the expansion, we need to choose
from each factor so that
. But we also know that in the
‘th factor, we have terms of the for
. In other words, we simply pick
so that
, which is exactly the
-adic representation of
. The coefficient on each of these terms if precisely
, and so taking the product gives the result.






